MAPLEQ is an extension for Google Chrome and Chromium Web Browsers which add extended support of Maple Computer Algebra system to Maple.TA system.
Currently, Maple.TA 2016 and 2017 versions are supported.
You can download and install MAPLEQ from Chrome Web Store.
DurackPL.com
| • Warning | ||
| • Requirements | ||
| • Quick Start | ||
| • MQ Markup |
Next: Requirements, Previous: Top, Up: Top [Contents]
MAPLEQ is in its alpha stage! Use it at your own risk!
Also observe the following while using MAPLEQ:
MAPLEQ generally tracks changes you apply to to files directly through Dropbox such as (a) file rename; (b) file move within a directory or between directories.
However, MAPLEQ does not track deletions. If you intend to delete a file in your Dropbox which was created by MAPLEQ, make sure that the corresponding question in Maple.TA is deleted first.
Opening a Maple.TA question created by MAPLEQ with MAPLEQ after the corresponding file in Dropbox is deleted is not recommended.
If you uninstall MAPLEQ, the above correspondence will be lost.
If you have multiple copies of Google Chrome or Chromimum Browser across different desktops and/or laptops and each copy has MAPLEQ extension installed, then the data listed above will be syncronised if and only if each instance of your browser is logged into your Google Account and data sync is enabled in your account settings.
If you do not like this arrangement, you are recommended to choose one dedicated copy of Google Chrome or Chromium Browser to use with MAPLEQ extension.
Next: Quick Start, Previous: Warning, Up: Top [Contents]
Google Chrome Browser or Chromium BrowserMAPLEQ is the extension which runs within Google Chrome or Chromium Browser
Dropbox accountMAPLEQ stores your data in your Dropbox. MAPLEQ will request access permission to your Dropbox the first time such permission is needed. MAPLEQ uses app permission which allows access to a dedicated directory in your Dropbox.
You can always revoke such permission at later stage. If you keep MAPLEQ files at the time you revoke your permission, then, if, for any reason, you decide to re-instate such permissions later, the MAPLEQ will continue work as if the permission had never been revoked.
Google Account (optional)MAPLEQ stores internal data such as correspondence between Maple.TA questions and Dropbox files and Dropbox access credentials in your Google Chrome or Chromimum Browser. If you would like to syncronise this data across multiple copies of browsers and use MAPLEQ extension in each such copy, you will need to log in every such browser into your Google Account and make sure that data sync option is enabled.
Alternatively, you can have one dedicated copy of Google Chrome or Chromium Browser with MAPLEQ extension installed.
Next: MQ Markup, Previous: Requirements, Up: Top [Contents]
Here is a few usage examples which will help you start making your own questions.
In the video below I show how to create from sratch the question which tests students understanding of the method of finding square root of a complex number.
This is the screenshot of the question content and the preview.
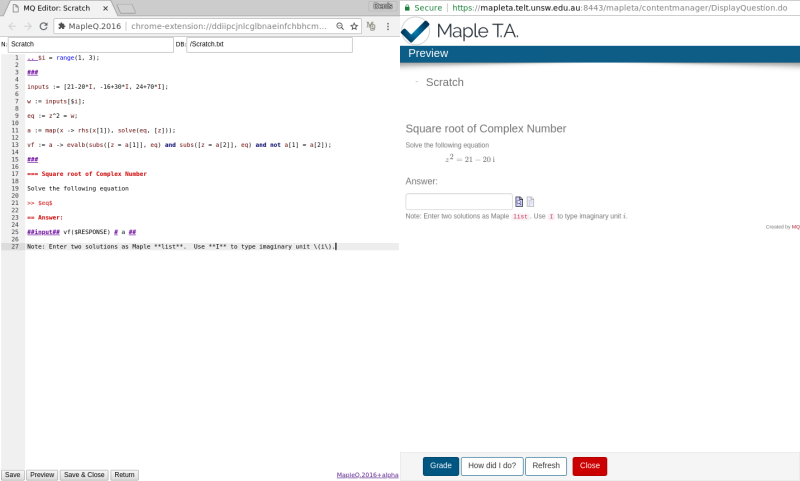
Here is the content if you need to copy-paste.
.. $i = range(1, 3); ### inputs := [21-20*I, -16+30*I, 24+70*I]; w := inputs[$i]; eq := z^2 = w; a := map(x -> rhs(x[1]), solve(eq, [z])); vf := a -> evalb(subs([z = a[1]], eq) and subs([z = a[2]], eq) and not a[1] = a[2]); ### === Square root of Complex Number Solve the following equation >> $eq$ == Answer: ##input## vf($RESPONSE) # a ## Note: Enter two solutions as Maple **list**. Use **I** to type imaginary unit \(i\).
Here is the video which showcase the capabilities of MAPLEQ extension. I use the question which designed to test students understanding of factorisation methods.
Here is the screenshot of the question content and preview.
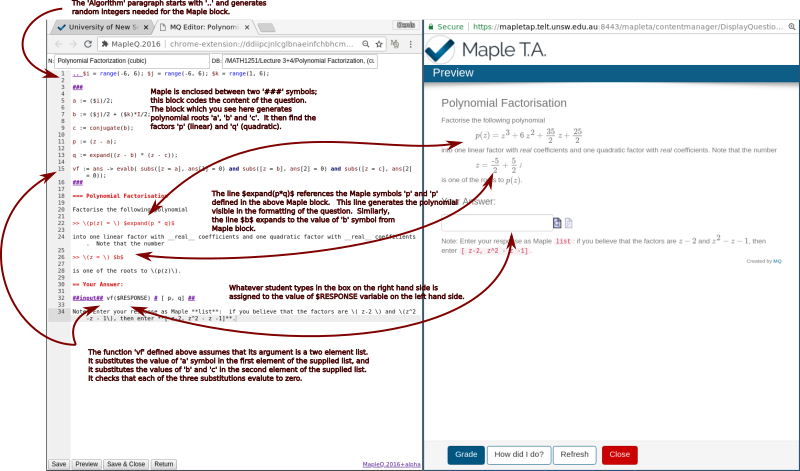
Here is the question content for copy-paste.
.. $i = range(-6, 6); $j = range(-6, 6); $k = range(1, 6); ### a := ($i)/2; b := ($j)/2 + ($k)*I/2; c := conjugate(b); p := (z - a); q := expand((z - b) * (z - c)); vf := ans -> evalb( subs([z = a], ans[1] = 0) and subs([z = b], ans[2] = 0) and subs([z = c], ans[2] = 0)); ### === Polynomial Factorisation Factorise the following polynomial >> \(p(z) = \) $expand(p * q)$ into one linear factor with __real__ coefficients and one quadratic factor with __real__ coefficients. Note that the number >> \(z = \) $b$ is one of the roots to \(p(z)\). == Your Answer: ##input## vf($RESPONSE) # [ p, q] ## Note: Enter your response as Maple **list**: if you believe that the factors are \( z-2 \) and \(z^2 -z - 1\), then enter **[ z-2, z^2 - z -1]**.
Here is another demonstration of making a question from scratch. The question tests students ability to do complex arithmetic in Cartesian form.
The screenshot of the MAPLEQ editor and the corresponding Maple.TA preview.
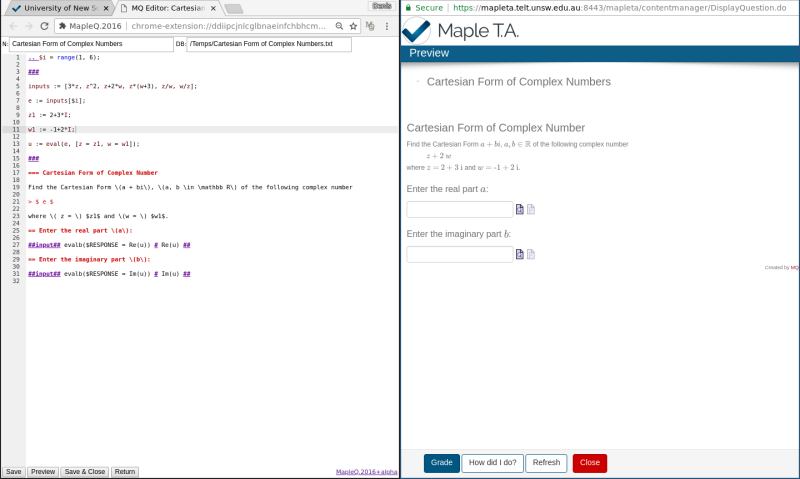
Here is the content of the question if you need copy-paste.
.. $i = range(1, 6); ### inputs := [3*z, z^2, z+2*w, z*(w+3), z/w, w/z]; e := inputs[$i]; z1 := 2+3*I; w1 := -1+2*I; u := eval(e, [z = z1, w = w1]); ### === Cartesian Form of Complex Number Find the Cartesian Form \(a + bi\), \(a, b \in \mathbb R\) of the following complex number > $ e $ where \( z = \) $z1$ and \(w = \) $w1$. == Enter the real part \(a\): ##input## evalb($RESPONSE = Re(u)) # Re(u) ## == Enter the imaginary part \(b\): ##input## evalb($RESPONSE = Im(u)) # Im(u) ##
Previous: Quick Start, Up: Top [Contents]
MQ Markup is the language/syntax you need to use in order to design your questions using MAPLEQ extension. MQ Markup consists of a few formatting and command elements. All such elements are split into three categories:
embedded elementssuch elements stretch over one or more lines, they start with a keyword (at the beginning of a line) and finish with a keyword
paragraph elementssuch elements stretch over one or more lines; they start with a keyword (at the beginning of a line) and the end with one or more empty (or blank) lines; there is one exception to this rule. If a text starts with no known keyword and ends with an empty line, it is treated as a regular paragraph and it is formatted accordingly
inline elementssuch elements appear inside paragraph elements, they start with a keyword and end with a keyword
Maple element supplies the lines of Maple code which are executed in order to produce content for the corresponding question; content produced by every such section can be referenced by the following elements. You may have more than one maple section.
Every maple section starts with ### which must be the
first symbol on a line and ends with ### which must be
the last symbol on a line. A maple element may stretch over a
few lines.
### inputs := [3*z, z^2, z+2*w, z*(w+3), z/w, w/z]; e := inputs[$i]; z1 := 2+3*I; w1 := -1+2*I; u := eval(e, [z = z1, w = w1]); ###
Include element inserts the content of another MQ Markup file at the point where it appears; the file must be stored in Dropbox directly; the pathname of the file is relative to the location of the file being edited.
[[ path_to_file.txt ]]
MQ Markup supports three heading formatting as shown below; there must be a space between the opening keyword and the corresponding content.
=== Heading paragraph == Subheading paragraph = Subsubheading paragraph
MQ Markup supports three type of indentation and centering; there must be a space between the opening keyword and the corresponding content.
> indented paragraph >> double indented paragraph >>> centred paragraph
MQ Markup processor ignores everything which appears between
%% at the beginning of a line and up until an empty or
blank line is observed.
Paragraphs starting with the keyword .. followed by at
least one white space are Maple.TA algorithm commands. The
complete list of commands with documentation can be found
here.
These commands are the most useful to generate random integers. For example the following set of commands generate three distinct integers between 1 and 10 (inclusively). Make sure that semi-colons ; are correctly placed after every command.
.. $i = range(1, 10); $j = range(1, 10); $k = range(1, 10); condition: ne($i, $j); condition: ne($j, $k); condition: ne($i, $k);
To emphasize a sequence of words inside the paragraph use
__ keyword around the selected sequence of words.
The following word is __emphasized__.
In order to typeset a sequence of words inside a paragraph use ** keyword around the selected sequence of words.
The following word is **typeset**.
This element generates code and formatting which accepts student response, verifies the response correctness and displays correct answer.
##input## maple test # maple answer ##
Each ‘maple test’ and ‘maple answer’ is a sequence of maple
commands. The ‘maple test’ sequence may reference $RESPONSE
value which evaluates to student response. The last statement in
‘maple test’ must return a Boolean value. If the value is
true, student answer is correct, otherwise incorrect. The
sequence of commands ‘maple answer’ must evaluate to the
correct answer which is shown to students.
The following example expects students to enter two functions as a
two-element Maple list [x(t), y(t)] and verifies whether
those two functions satisfy the equation F(x(t), y(t)) = 0
under the assumption that trigonometric simplifications can be
used.
##input## evalb( simplify(subs([x, y] =~ $RESPONSE, F(x, y)), trig) = 0)
# [ x(t), y(t) ] ##
Input element corresponds to the following Maple.TA source section:
...
mode=Maple@
type=maple@
allow2d=0
...
Note that the setting allow2d=0 corresponds to "text-entry"
mode. Switching to allow2d=2, will enable "symbolic-entry"
mode. See Maple Syntax for further details.
This element is almost identical to ‘input element’, with the
following modifications: (a) student response is referenced by
response value; (b) it accepts the third argument ‘hidden
names’ which is a comma separated list of Maple names
(mostly functions) which are rendered empty while evaluating
student response.
##input2## maple test # maple answer # hidden names ##
Here is an example which expect student to correctly enter the
Real part of the cube of a complex number but ensures that the
student cannot use functions Re and Im in his typed
response.
### u := (1 -3*I)^3; ### ... ... ##input2## evalb(response = Re(u)) # Re(u) # Re,Im ##
This element is identical to input element with one exception: student input will not be processed by Maple.TA.
For instance if a student enters ’1 + 2’ in input element and clicks ’preview’ button, Maple.TA process will simplify the expression and shows ’3’. That is, ’3’ will be taken as student answer.
On the other hand, typing ’1 + 2’ in formula element will
do no simplifications and the answer will be taken literally as ’1
+ 2’.
Please note that Maple.TA simplifying engine is relatively advanced. For instance, typing ’I^2’ will be simplified to ’-1’ using Complex Numbers arithmetic. Therefore, if the purpose of your question to test knowledge of basic Complex Arithmetic, then formula element is your choice.
Formula element corresponds to the following Maple.TA source section:
...
mode=Maple@
type=formula@
allow2d=1
...
See Maple-graded Formula for further details.
This is the analogue of input2 element with respect to formula element.
That is, this element will accept student input literally with no
simplifications applied and hide every Maple function which
is listed within this element.
Generates code and formatting for multiple choice response. Here is an example, which offers a choice between three equations. The correct response (marked with !!) is the second response. Multiple marks !! are permitted.
### F[1] := ($a) * z = x^2 + ($b)^2*y^2; F[2] := ($a)^2 * z^2 = ($b)^2*x^2 + y^2; F[3] := x^2/($a)^2 + y^2 = ($b)^2; ### .... .... ##choice## $F[1]$ # !! $F[2]$ # $F[3]$ ##
Each argument of choice element is a processed by paragraph processor, in particular, every such argument accepts inline elements.
Generates code which inspect student to match a series of answers with a series of questions. The following example expects match between quadratic surface equations with the corresponding names.
### F[1] := 2*z = x^2 + y^2; F[2] := 4z^2 = 2*x^2 + y^2; F[3] := 4*x^2 + y^2/4 + z^2 = 1; F[4] := x^2/4 + y^2 = 4; F[5] := x^2 + y^2 - 4 * z^2 = 1; F[6] := x^2/4 - y^2 - z^2 = 1; F[7] := 2 * z = x^2 - 4*y^2; ### .... .... ##match## $F[1]$ === paraboloid, elliptic # $F[2]$ === cone # $F[3]$ === ellipsoid # $F[4]$ === cylinder # $F[5]$ === hyperboloid, one sheet # $F[6]$ === hyperboloid, two sheets # $F[7]$ === paraboloid, hyperbolic ##
Each argument of match element is a processed by paragraph processor, in particular, each such argument accepts inline elements.
The following plot commands are supported:
##plot## arg1 # arg2 # ... # argN ## ##implicitplot## arg1 # arg2 # ... # argN ## ##domainplot## arg1 # arg2 # ... # argN ##
The commands and the arguments are directly mapped to the
following maple commands: plot, plots[implicitplot] and
plots[inequal].
The following command plots ‘x=1’ section of elliptic paraboloid and replaces ‘y’ and ‘z’ symbols with ‘u’ and ‘v’.
##implicitplot## subs([x = 1, y = u, z = v], z = x^2 + 4*y^2) #
u = -5 .. 5 #
v = -5 .. 5 #
rangeasview = true #
gridrefine = 2 ##
You use maple expression element to insert math formatted maple value into the text of your question. The following example inserts the integral symbol.
### A := Int(sin(x), x=-Pi..Pi); ### ... ... Evaluate the integral $A$.
You use latex element to insert static math encoded using latex syntax. This is formatting command only, it cannot reference maple expressions.
Find real part of a complex number \(z \in \mathbb C\)